How To Create A 2d Matrix In Python

Get FREE domain for 1st year and build your brand new site

Array is a linear data structure consisting of list of elements. In this we are specifically going to talk about 2D arrays. 2D Array can be defined as array of an array. 2D array are also called as Matrices which can be represented as collection of rows and columns.

In this article, we have explored 2D array in Numpy in Python.

index

NumPy is a library in python adding support for large multidimensional arrays and matrices along with high level mathematical functions to operate these arrays.

Benefits of Numpy :

Numpy are very fast as compared to traditional lists because they use fixed datatype and contiguous memory allocation.
Numpy has lot more functions.

Installing NumPy in windows using CMD

                pip install numpy

The above line of command will install NumPy into your machine.

Basics of NumPy

For working with numpy we need to first import it into python code base.

                import numpy as np

Creating an Array

Syntax -
Create-1

                arr = np.array([2,4,6], dtype='int32') print(arr)

[2 4 6]

In above code we used dtype parameter to specify the datatype

To create a 2D array and syntax for the same is given below -

                arr = np.array([[1,2,3],[4,5,6]]) print(arr)

[[1 2 3]
[4 5 6]]

Various functions on Array

Get shape of an array

                arr.shape

(2, 3)

Get Datatype of elements in array

                arr.dtype

dtype('int64')

Accessing/Indexing specific element

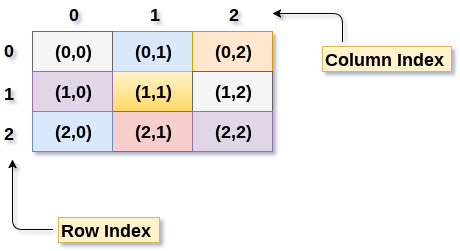
To get a specific element from an array use arr[r,c]
here r specifies row number and c column number.

                arr[1,1]

5

To get all elements of Row or Column
: is used to specify that we need to fetch every element.

                arr[1,:] #This will return all elements of 1st row in the form of array

array([4, 5, 6])

Accessing multiple rows and columns at a time

                arr = np.ones((4,4)) t = arr[1:3,1:3] print(t) # t will be a 2x2 matrix with 4 elements

[[1. 1.]
[1. 1.]]

Initializing different types of an array

There are various built-in functions used to initialize an array
Zeros Array
zeros((r,c)) - It will return an array with all elements zeros with r number of rows and c number of columns.

                arr_zeros = np.zeros((3,5)) print(arr_zeros)

[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]

Ones Array
Similar to zeros we can also have all elements as one by using ones((r,c))

                arr_ones = 2*np.ones((3,5)) print(arr_ones)

[[2. 2. 2. 2. 2.]
[2. 2. 2. 2. 2.]
[2. 2. 2. 2. 2.]]

Random Array
random.rand(r,c) - this function will generate an array with all random elements.

                arr_rand = np.random.rand(3,4) print(arr_rand)

[[0.12684248 0.42387592 0.0045715 0.34712039]
[0.3431914 0.51187226 0.59134866 0.64013614]
[0.91716382 0.35066058 0.51826331 0.9705538 ]]

Identity
identity(r) will return an identity matrix of r row and r columns.

                arr_i = np.identity(3) print(arr_i)

[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]

Operations on 2D array

Arithmetic Operations
Applying scalar operations to an array.

                a = np.array([[1,2,3],[4,6,2],[0,7,1]]) #array with size 3x3  #Scalar operation - It will operate with scalar to each element of an array print(a+2) print(a-4) print(a*3) print(a/2) print(a**2)

[[3 4 5]
[6 8 4]
[2 9 3]]

[[-3 -2 -1]
[ 0 2 -2]
[-4 3 -3]]

[[ 3 6 9]
[12 18 6]
[ 0 21 3]]

[[0.5 1. 1.5]
[2. 3. 1. ]
[0. 3.5 0.5]]

[[ 1 4 9]
[16 36 4]
[ 0 49 1]]

Matrix operation for 2D matrix

                a = np.array([[1,2,3],[4,6,2],[0,7,1]]) #array with size 3x3 b = np.array([[3,6],[1,4],[7,2]]) #array with size 3x2 c = np.array([[1,0,3],[2,3,1],[0,0,1]]) add = a+c mul = np.matmul(a,b) #Matrix multiplication of a and b  print(add) print(mul)

[[2 2 6]
[6 9 3]
[0 7 2]]

[[26 20]
[32 52]
[14 30]]

Finding Minimum and Maximum from all elements

                np.min(b)

1

                np.max(b)

7

Finding determinant of a Matrix

                np.linag.det(a)

68.00000000000001

Sum of elements along the column and row

                #To add all elements of a column np.sum(b,axis=0)

array([11, 12])

                #To add all elements of a row np.sum(b,axis=1)

array([9, 5, 9])

Reorganizing Array

Changing shape of an array

                before = np.array([[1,2,3,4],[5,6,7,8]]) #it's dimensions are 2x4 after = before.reshape(4,2) #it's dimensions are 4x2 print(after)

[[1 2]
[3 4]
[5 6]
[7 8]]

Horizontal Stacking - Concatinating 2 arrays in horizontal manner

                a = np.identity(2) b = np.array([[1,2],[2,1]]) np.hstack((a,b))

array([[1., 0., 1., 2.],
[0., 1., 2., 1.]])

Vertical Stacking - Concatinating 2 arrays in vertical manner

                a = np.identity(2) b = np.array([[1,2],[2,1]]) np.vstack((a,b))

array([[1., 0.],
[0., 1.],
[1., 2.],
[2., 1.]])

Question

If we have a 4x4 Identity Matrix named as 'eye' then how would you obtain another 2x2 identity matrix from it.

eye[0:2,0:2]

eye[1:0,0:1]

eye[0:1,0:1]

eye[1:2,1:2]

As we want first two rows and columns we will start indexing from 0 and it will end at 2.